H = (GF/21/2) ò d3x [u†(x) g°gm n(x)] [e†(x) g°gm n(x)] .

A causa del piccolo valore di (v/c)2 nei decadimenti b (circa 10-6), le piccole componenti degli spinori nella corrente adronica sono trascurabili, cosicché questa può essere scritta come u†(x) n(x), dato che solo il termine con m = 0 contribuisce. Le interazioni descritte da questo prodotto non possono modificare lo spin dei nucleoni, e l'hamiltoniano di Fermi non può descrivere tutti i decadimenti nucleari, alcuni dei quali sono governati da transizioni alla Gamow-Teller, in cui si ha DJ = 1 (spin flip dei nucleoni). Ferma restando l'idea del prodotto invariante fra correnti, si devono pertanto considerare anche le altre correnti possibili se si vuole una teoria completa dei decadimenti nucleari. Quelle con definite proprietà di trasformazione sono la corrente scalare S, la vettoriale V, la assiale A, e la tensoriale T: per la parte adronica esse sono definite dalle relazioni seguenti:

S: u†(x) n(x)

V: u†(x) g°gm n(x)

A: u†(x) g°gmg5 n(x)

T: u†(x) g°smn n(x).

Nell'approssimazione non relativistica, le correnti S e V danno transizioni alla Fermi, e si riducono a u†(x) n(x); e le correnti A e T danno transizioni alla Gamow-Teller, essendo scrivibili come u†(x)si n(x) (si sono le matrici di Pauli). Fu possibile dimostrare, dalla linearità della relazione fra energia dell'elettrone emesso nei decadimenti b e la funzione pe-1 dG/dpe - ove G è la frequenza di decadimento - che l'interazione debole che governava i decadimenti b doveva coinvolgere una sola corrente per le due classi (S,V) e (T,A). A causa di ciò, negli anni '50 vi fu uno studio intenso di reazioni deboli che permettessero di decidere quale fosse la forma esatta di H.

Nel 1956 avvenne però un fatto importantissimo per la comprensione delle interazioni deboli. Lee e Yang, mossi dalla strana eguaglianza di massa e vita media degli stati allora denominati t e q, che decadevano in stati a parità opposta, effettuarono un approfondito studio dei risultati sperimentali sulle interazioni deboli, dal quale emerse che da nessun esperimento fino ad allora eseguito sarebbe stato possibile evincere la non conservazione della parità nelle interazioni deboli: per discriminare fra eventi a parità conservata o violata andavano osservate quantità con proprietà di trasformazione pseudoscalari, come il prodotto fra vettori polari e vettori assiali.

Pochi mesi dopo il sasso lanciato nello stagno da Lee e Yang, arrivarono i primi risultati sperimentali, da Wu e collaboratori, che mostrarono come effettivamente la parità fosse violata -e massimalmente- nelle interazioni deboli. Ciò implicava l'introduzione in H di un fattore (1±g5), cosicché l'hamiltoniana avrebbe potuto scriversi in una forma del tipo

H = (GF/21/2) ò d3x Si=S,V,... { Ci[u†(x)g°Gi n(x)] [e†(x) g° Gi (1±g5) n(x)] }.

ove ho indicato con Gi le varie combinazioni di matrici g. La matrice (1±g5) non è altro (a parte un fattore 1/2) che la rappresentazione di Dirac dell'operatore che proietta sugli stati di elicità levogira, Pl (se il segno è negativo) o destrogira, Pr (se è positivo): ciò implica che il neutrino deve avere elicità definita. Se il neutrino è levogiro, il fattore che rende non nullo l'hamiltoniano è quello con il segno negativo, e le matrici Gi di tipo S e T danno contributo nullo ad H (perché anticommutano con Pl): in tal caso l'interazione debole è combinazione di correnti vettori e assiali. Se viceversa il neutrino è destrogiro, sono S e T le correnti che giocano un ruolo nell'interazione debole.

Determinare lo stato di elicità dei neutrini - particelle che hanno sezioni d'urto di scattering con i nucleoni dell'ordine di G2s - può sembrare un'impresa disperata. Ma questo fu possibile nel 1958 a Goldhaber, Grodzins e Sunyar in un esperimento che per profondità di concezione e semplicità dell'arrangiamento va considerato una pietra miliare della fisica delle particelle elementari - a mio parere ancora più del rivoluzionario esperimento che permise alla signora Wu la determinazione dell'anisotropia dell'emissione degli elettroni nei decadimenti di cobalto polarizzato, che pure le valse il premio Nobel.

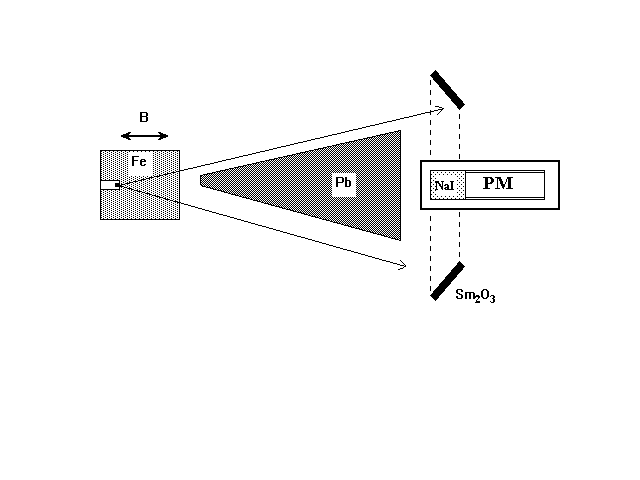
Ma non è finita qui: come si misura la polarizzazione dei fotoni, se non vogliamo influenzarne la successiva interazione con il bersaglio di Sm2O3 ? Non certo magnetizzando il bersaglio, dato che i nuclei di Samario hanno J=0. Qui viene l'ultimo colpo di scena: lo si può fare con grande semplicità, facendo attraversare ai fotoni, prima che questi giungano al bersaglio di Samario, del ferro magnetizzato lungo l'asse di quantizzazione. Nel ferro magnetizzato gli elettroni hanno lo spin in gran parte allineato al campo magnetizzante. Questi elettroni potranno interagire per spin flip con i fotoni emessi dal Samario solo se il loro spin è inizialmente opposto a quello dei fotoni: basta allora misurare la frequenza di scattering risonante con il campo magnetizzante nella direzione positiva o negativa di moto dei fotoni, e confrontare questi due numeri, e il gioco è fatto. Per capirlo esaminiamo il caso in cui i neutrini siano destrogiri: i fotoni emessi in avanti avranno allora polarizzazione -1, ed arriveranno al Samario in maggior numero se il campo nel ferro è opposto alla loro direzione di moto. Dovremmo allora osservare una maggior frequenza di scattering risonante con il campo nella direzione opposta al moto dei fotoni. Goldhaber, Grodzins e Sunjar trovarono invece una maggior quantità di scattering risonante con il campo nel verso di moto dei fotoni: il neutrino ha elicità levogira, e le interazioni deboli hanno un'hamiltoniana con correnti vettoriali e assiali.

Ritengo sia doveroso sottolineare l'ingegno di Goldhaber, Grodzins e Sunjar, che ha permesso la rivelazione di una proprietà così effimera come il verso di polarizzazione dei neutrini - particelle tra le più sfuggenti e difficili da studiare - attraverso un banale conteggio di impulsi in un tubo fotomoltiplicatore !